図Bを円錐、円柱、半球の3つの部分に分けて それぞれの体積の和をだす。 (例2) l 図C l 図D 図Cを直線lを軸に一回転させると図Dになる。 図Dは円錐の内側に細い円錐型の空間がある形。 外側の円錐から、内側の空間の小さい円錐を 引く 。 錐形 の体積は 柱形 の体積の 3分の1 である性質 円錐は、 錐体 の一種である。 高さを h 、母線の長さを c 、底面の半径を r 、底面積を B (= π r2 )、底面の周を b (= 2 π r )、 と置けば、円錐の側面積 Sside 、表面積 S 、 体積 V はそれぞれ以下で与えられる : S s i d e = π r c = π c c 2 − h 2 = 1 2 b c {\displaystyle S_ {\mathrm {side} }=\pi rc=\pi c {\sqrt {c^ {2}h^ {2}}}= {\frac {1} {2}}bc}

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
円錐 形 体積
円錐 形 体積-円柱 , 円錐 , 円柱と円錐の違い , 円柱の特徴 , 円錐の性質 , 円柱の展開図 , 円錐の展開図 , 『教科書 中学校 数学Ⅰ』 数研出版 『やさしくまるごと中学数学』 吉川直樹 Gakken この科目でよく読まれている関例 3 65 (円錐の体積) 底面の半径 ,高さ の円錐の体積は である. これを多重積分で求める. 円錐の底面は 平面にあるとし, その領域を



円錐とは 体積 表面積の公式や求め方 受験辞典
回転体の体積は積分の公式から簡単に求めることができる。 球欠+円錐の体積 扇形の回転体2 倍角と半角の関係 次へ 回転体の体積 関連トピック 不定積分;変数変換により円錐の体積を多面的に捉える課題 ―高等学校第2学年数学Ⅱ「3次関数の最大最小」の指導を通して― (実践者 新潟県立十日町高等学校 堀越 康裕) 「濾紙を操作し、連続的に可変させて円錐の形をいろいろ作らせるシンプルな具体的活動」を通して 円錐の体積の最大値を、3次 三角錐,四角錐,円錐,の錐 (すい)という漢字は訓読みでは「きり」と読みます.これは,小さな穴を開けるための先のとがった工具です. 三角錐や円錐といった「錐」とは,穴をあける道具のように先の尖った立体です. では,「〇〇錐」の体積の求め方はどうだったかというと, (〇〇錐の体積) = (底面積)× (高さ)× 1 3 ( 〇〇錐の体積) = ( 底面積) ×
体積 = 底面積 × 高さ ÷ 3積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない(円錐でも三角錐でも四角錐でも適用可能)証明方法です。 円錐の場合、底面は円の形となるので、底面積部分に円の面積公式を代入することによって、円錐の公式を完成させることができます。 ここで、「錐の体積」の公式を一度理解しておけば、 三角錐 、四角錘などの公式を考える際に関連付けて理解することが可能となります。
ガラス器具/体積計 遠心沈殿管 円錐形 Centrifuge Tubes, conical bottom ・遠心分離に使用する容量が10mLの細い円錐状の容器です。 ・目盛つきと目盛なしがあります。 品目コード別情報 (仕様) A A この製品を比較表に追加する;底が楕円として、楕円錐の体積を算出したかった。 keisanより 長径a,短径bの楕円の面積S=πab、半径rの円の面積はS=πr 2 ですので、直円錐の体積の半径rに開平√(a*b)を計算して代入すれば、楕円錐の体積が求まります。 ・体積の公式は立方体の体積から考える! ・比を使って他の形にも応用可能! ・高校の「積分」でも公式は作れる! ということでした! どうでしょう、公式に関してすっきりできましたか? ぜひこの考え方をマスターして、友達をぎゃふんといわせ




裏技 プリン型の立体の体積 一瞬で求められますか Youtube




写真の問題が分かりません Clear
円錐は展開図にすると,円と扇形に分離されるのでこのような公式になります. 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います. 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて,次は円錐の体積を求める公式です.円錐の底面は円になっていますので、 円の面積 を計算する式と高さを使えば体積を求めることができます。 円錐の底面積と高さを掛け合わせましたら、後はその値を3で割ってください。円錐体形鏡板の内面の表面積・全体容量及び製品重量(角度:ラジアン) 各部の記号と名称 D:大径部の内径 R:大径部の丸みの内半径 h1:大径部のフランジ長さ d:小径部の内径 r:小径部の丸みの内半径 h2:小径部のフランジ長さ t:厚さ
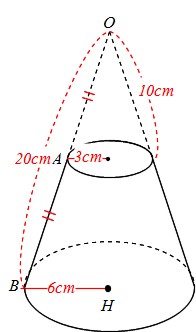



Math 円錐 円錐台と面積比 体積比 働きアリ



円錐形の容器に 深さ3 1まで水を入れたとき 水の体積と容器の容積比は Yahoo 知恵袋
円錐の体積は、次の公式で求められます。 円錐の体積=底面積×高さ÷3 円錐の底面積は円の面積ですので、円の面積×高さ÷3で求めることができます。 ⇒ 円の面積の求め方 スポンサードリンク 円錐の体積を求める問題よって、小さな円錐の体積は、 $\pi b^2\times\dfrac{bh}{ab}\times\dfrac{1}{3}=\dfrac{\pi b^3h}{3(ab)}$ です。 一方、大きな円錐の高さは、 $xh=\dfrac{bh}{ab}\dfrac{(ab)h}{ab}=\dfrac{ah}{ab}$ となります。 したがって、大きな円錐の体積は、製品写真 品目コード A 型式 容量mL 10 外径mm




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



円錐とは 体積 表面積の公式や求め方 受験辞典
角柱 と 双角錐 は互いに 双対多面体 だが、 円柱 と双円錐の間にはそのような関係はないので注意が必要である。 表面積 S 、 体積 V は、高さを h 、母線の長さを c 、赤道面の半径を r 、赤道面の面積を E 、赤道面の周を e と置けば S = 2 π r c = 2 π r r 2 h 2 = e c {\displaystyle S=2\pi rc=2\pi r {\sqrt {r^ {2}h^ {2}}}=ec}体積の公式に当てはめて $$9\pi \times 4 \times \frac{1}{3}$$ $$=12\pi cm^3$$ となります。 半径がわからない場合でも 考え方は、高さを求めるときと同じですね! 円錐の体積を求める方法 まとめ お疲れ様でした! 円錐の体積を求めるときに 高さや半径がわから三角錐,四角錐,円錐の体積 V ∠ABC=90° だから,底面は直角三角形 でその面積は 8×6÷2=24 (cm 2) 三角柱の高さは AD=6 cm したがって,三角柱の体積は 24×6=144 (cm 3)(答) 以下の問題では,選択肢をクリックすると採点結果と解説が表示されます. 問題11 図1は,すべての辺の長




体積の求め方 計算公式一覧




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
体積の公式、円錐の体積の公式など下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積 円錐の体積と公式は?1分でわかる公式、問題と高さの求め方、証明 100円から読める!ネット不要!印刷しても読みやすいpdf記事はこちら⇒ いつでも3 円すいの体積を求める問題 問題2 図の円すいの体積を求めなさい。 問題の見方 立体の体積を求める公式より,~~すいとつく立体の場合, $$(底面積)×(高さ)×\frac{1}{3}=(体積)$$ で求められます。~~すいの立体のときは,$$\frac{1}{3}$$をかけ算するのがポイントです。 歪んだ円錐の体積を求める。 数学的に「歪んだ円錐」という立体が定義されているのか知らないので、次のように形状を定める。 円錐という形は円の中心の真上に錐体の頂点がある立体だけど、歪んだ円錐は中心の真上以外の所に頂点がある。 見れば見るほど、円錐の体積"底面積×高




円錐の体積の求め方 公式と計算例




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
・正方形や円などの面積,直方体の体積の求め方を 黒板にまとめておくとよい。 ・様々な柱体と錐体を見せ,円柱,円錐など名称を 言わせる。 展 開 1 ②円柱と円錐,四 角柱と四角錐の 体積の関係から, 同じ底面積で同 じ高さをもつ他 の立体(五角柱と 五角錐など)の体 積の関係を類推アズワンのaxel172 液量計(円錐形・ハイグラス) ml のコーナーです。axelは研究開発、医療介護、生産現場、食品衛生など幅広い分野に4万点以上の品揃えでお応えする商品サイト。3000円以上ご注文で送料無料。中3_三角形の相似_円錐の体積比(日本語版) Watch later Share Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations



円錐とは 体積 表面積の公式や求め方 受験辞典




公式を図解 すい体の体積 円すいの表面積の求め方
円錐の体積を求める公式は、 V = 1/3 Sh = 1/3 πr^2 h で表されます。このページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。それでは、他にも円錐の体積に関する問題に挑戦して 理解を深めていきましょう! 演習問題に挑戦しよう! 下の図のような円錐形の容器に3cm³の水を入れ、水面と容器の上の面が平行になるようにして深さを測ると、10㎝になった。水はあと何cm³入るか求めなさい。 解説&答えはこちら そして、底面積×高さ(h)=円柱の体積ですから、「36π×13=468π(cm3)」が答えです。これを公式化すると下のようになります。公式円柱の体積=底面積×高さ =半径×半径×円周率×高さ =πr2h =Shちなみに円錐の体積を求める公式もあります



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
円錐台の体積の公式 S:はじめまして。いつもホームページ読ませていただいてます。 さて、円錐の体積で教えてほしいことがあります。 円錐を底面からhの高さで底面と水平にスパッと切った時の体積なのですが、真横からみると台形になる。この立体の底面(大きい円)の面積をa、上面




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室
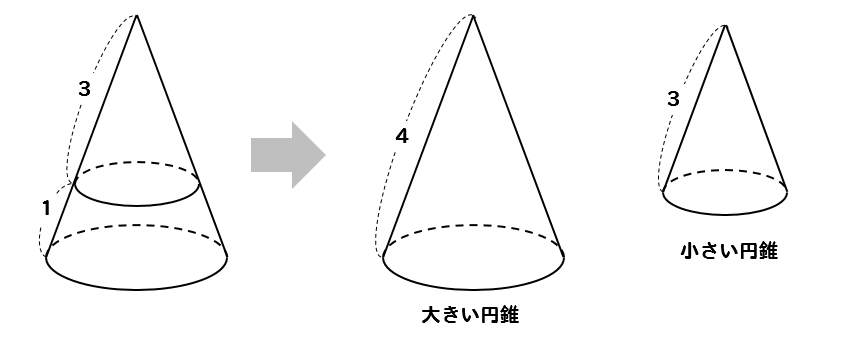



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



1




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




13 Cm13 Cm 10cm 10 Descubre Como Resolverlo En Qanda




角錐と円錐の体積 Youtube




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




毎日問題を解こう 27 苦手な数学を簡単に




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
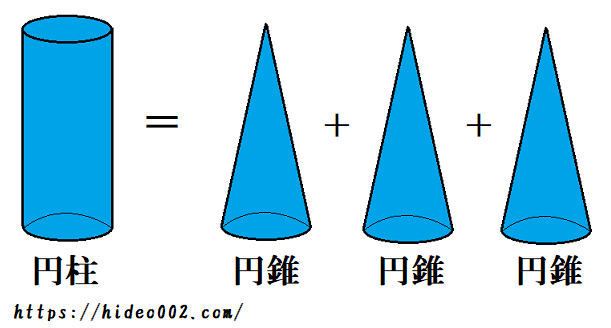



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋
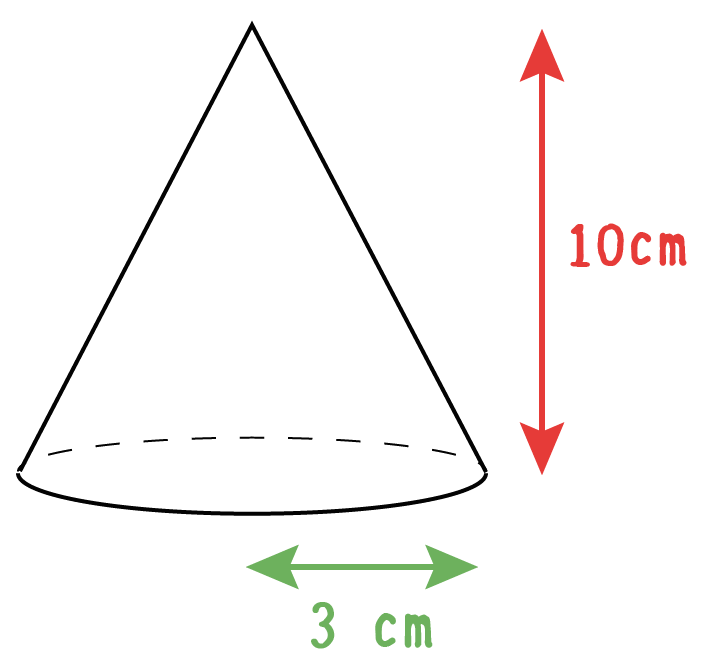



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




13 Cm13 Cm 10cm 10 Descubre Como Resolverlo En Qanda



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




中3 三角形の相似 円錐の体積比 日本語版 Youtube
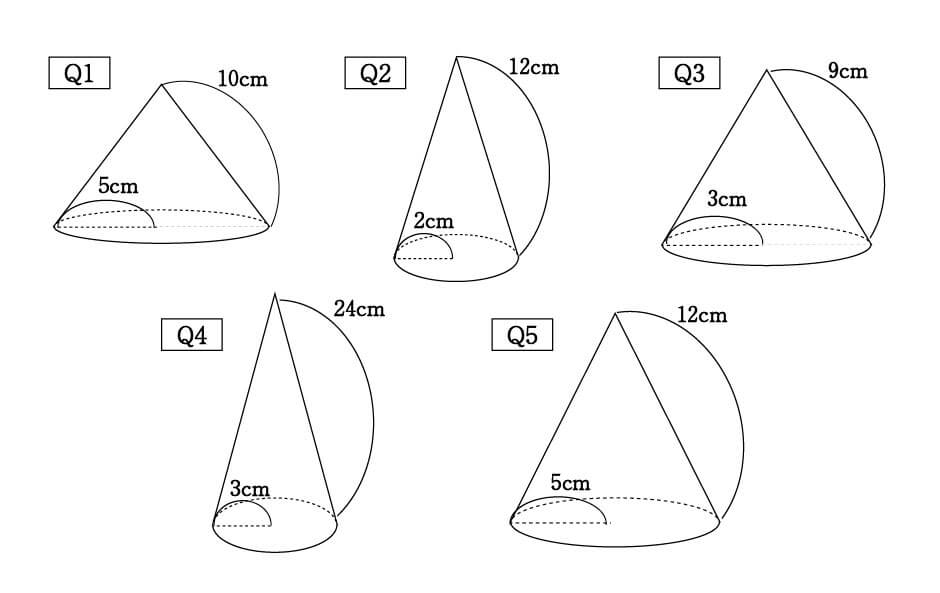



数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
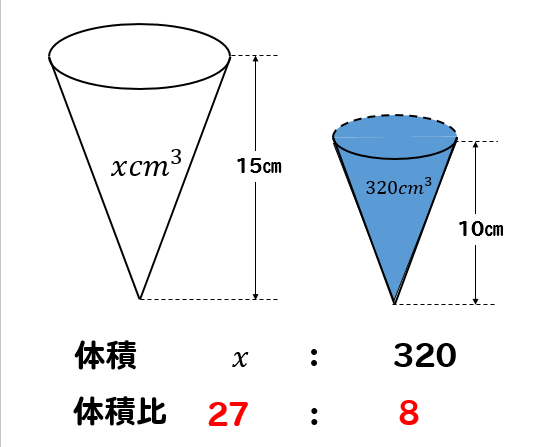



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ
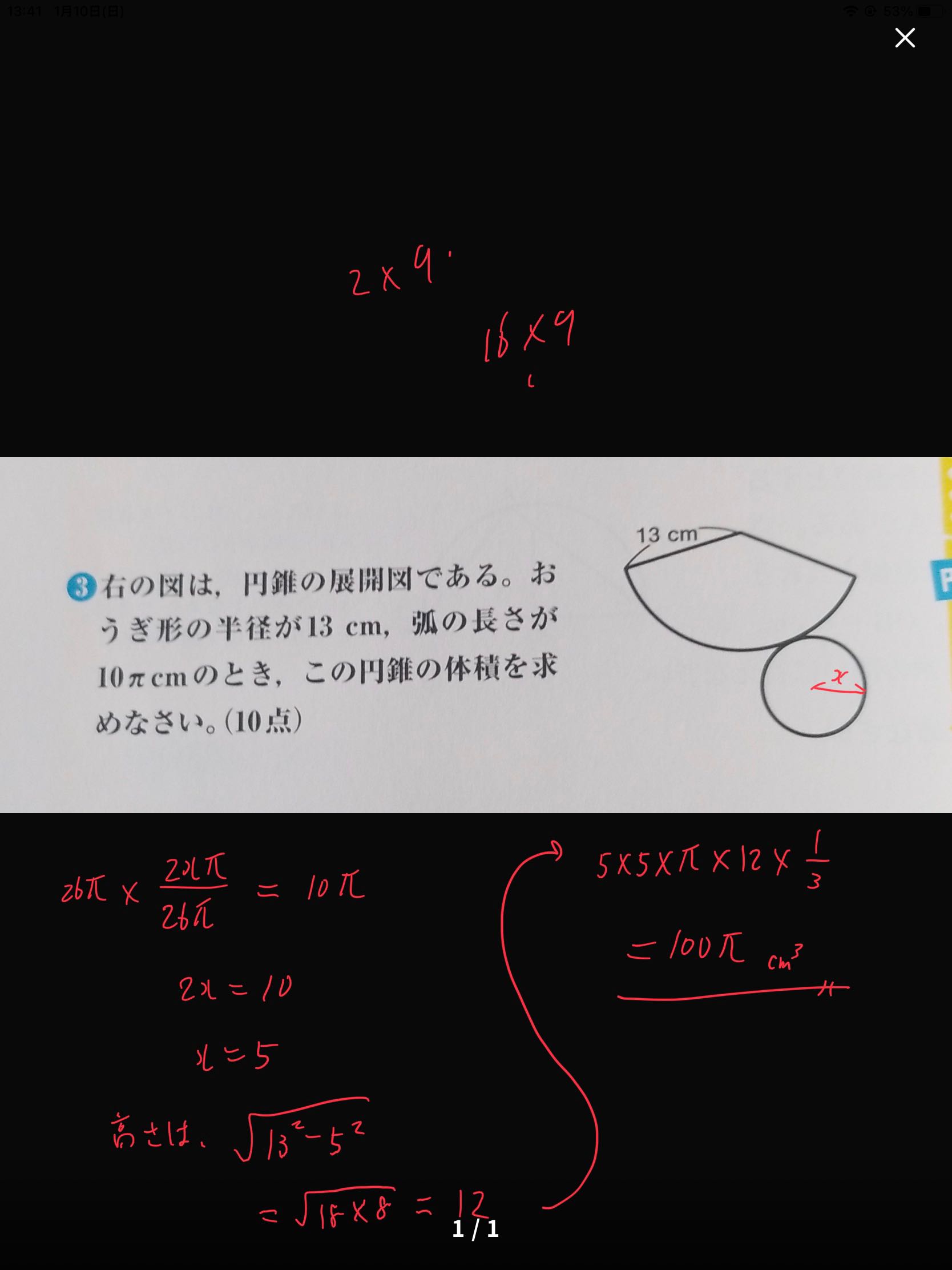



13 Cm13 Cm 10cm 10 Descubre Como Resolverlo En Qanda




相似比と体積比 円錐台 中学3年数学 Youtube
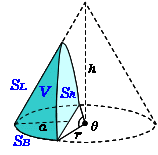



一部が欠けた直円錐の体積 高精度計算サイト




円錐の体積ってなんであの公式なの Webty Staff Blog
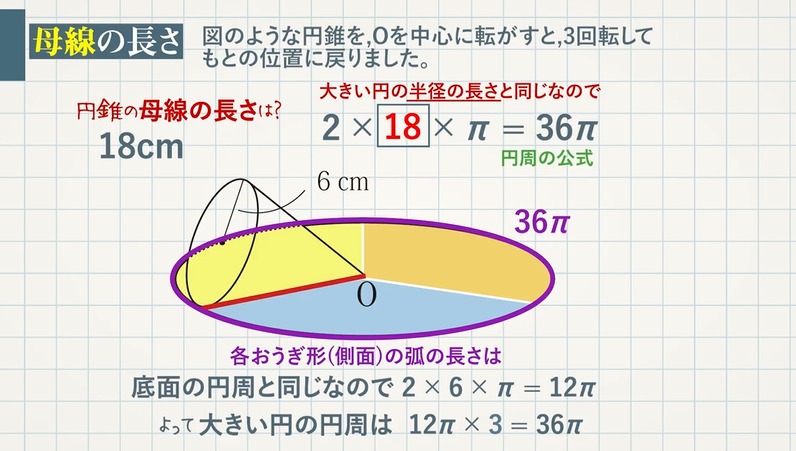



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




中学2年生です Clear




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



歪んだ円錐の体積 戯言




3月4日はバウムクーヘンの日なので 積分します 理系男子の独り善がり




円錐の体積を求める Youtube
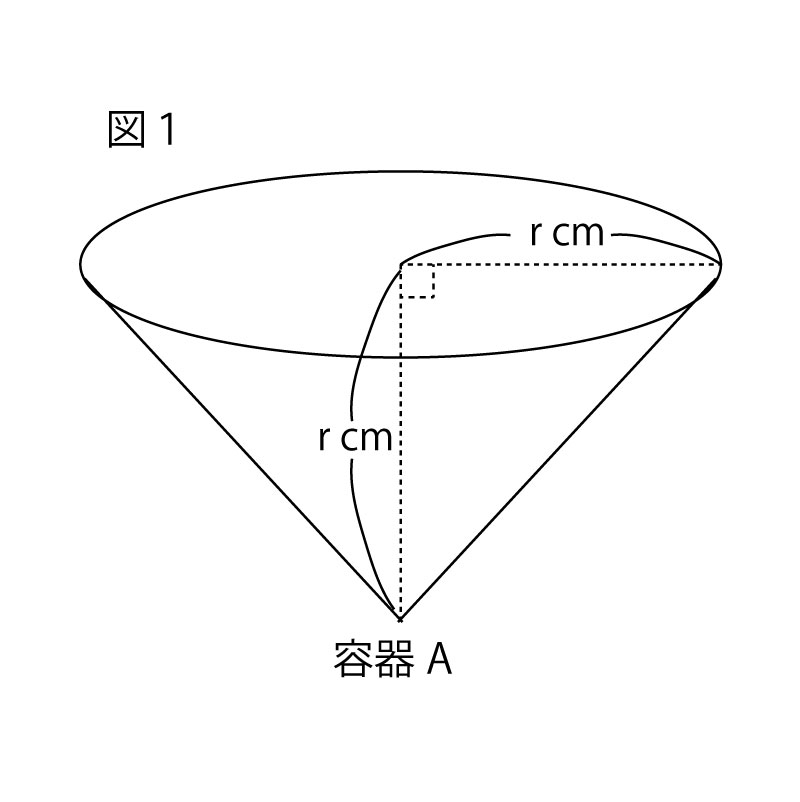



19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



1




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



円錐台 Wikipedia




角錐 円錐の体積と表面積の公式 数学fun
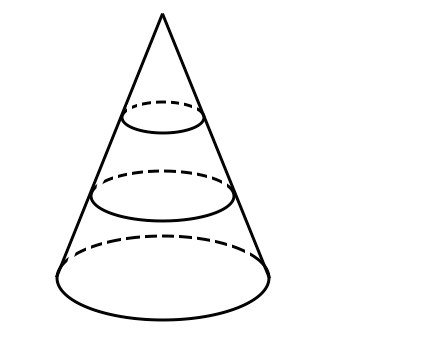



相似な図形 体積比 相似な図形に注目せよ 苦手な数学を簡単に




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook



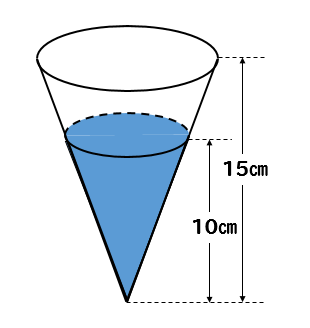
中学数学教えてください 図のような高さ15cmの円錐の形をした容器に水を Yahoo 知恵袋




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




角錐 円錐の体積と表面積の公式 数学fun




円錐の体積ってなんであの公式なの Webty Staff Blog




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




3d100 Lihat Cara Penyelesaian Di Qanda



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




公式を図解 すい体の体積 円すいの表面積の求め方



円錐とは 体積 表面積の公式や求め方 受験辞典




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学
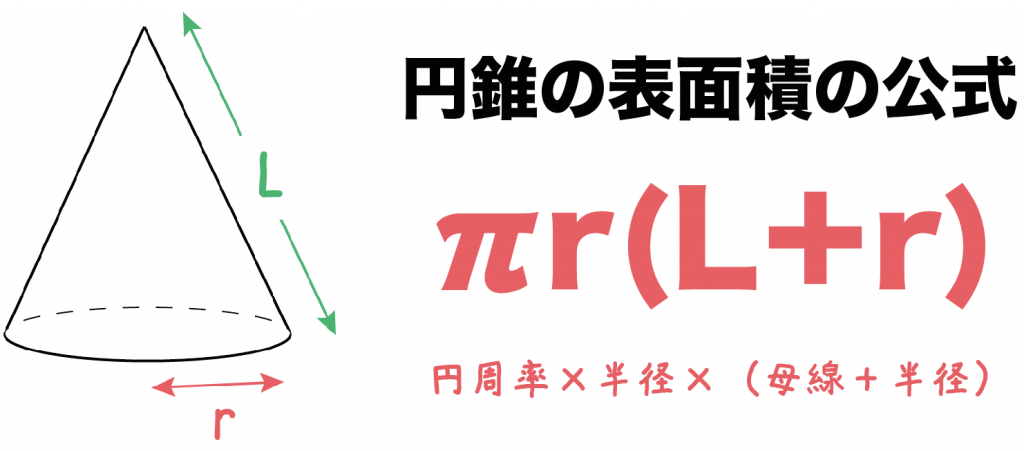



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の公式 数学fun




公式を図解 すい体の体積 円すいの表面積の求め方




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



1




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




実用数学技能検定 数検 おはようございmath 今日は10月25日 毎日25日は プリンの日 だそうです 一般的にプリンの形 は 円錐台ですね ということで プリンの表面積と体積を計算するための公式をお伝えしますね 実際に計ってみてください プリン
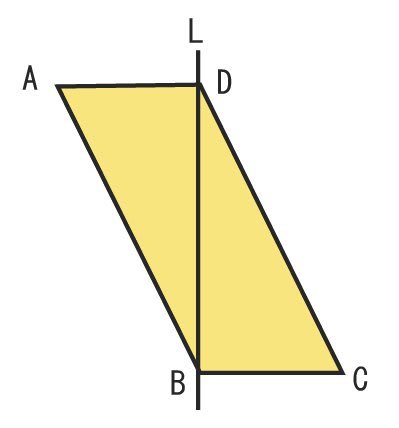



円錐を カット する 体積は どうなる 名寄 算数数学教室より




直円錐の体積 高精度計算サイト




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




公式を図解 すい体の体積 円すいの表面積の求め方




すいの体積はなぜ1 3か Youtube
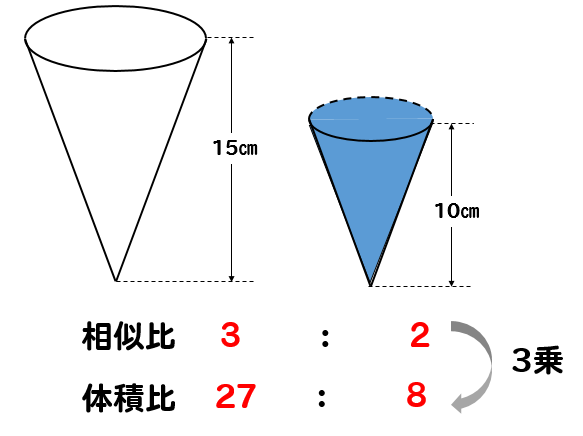



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円錐形の容器に 深さ3 1まで水を入れたとき 水の体積と容器の容積比は Yahoo 知恵袋
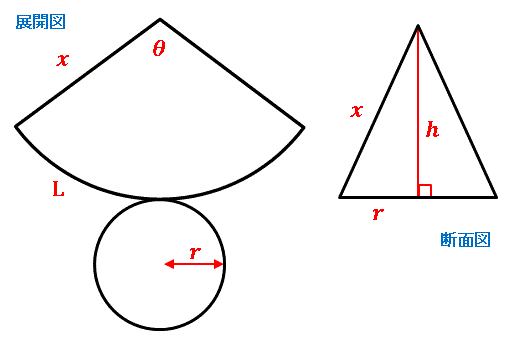



直円錐の体積




円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com



双円錐 Wikipedia




角錐 円錐の体積と表面積の公式 数学fun




円錐の表面積の求め方 公式と計算例



歪んだ円錐の体積 戯言




数学 中3 55 相似と体積 応用編 Youtube



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




一番最後の問題がわかりません 円錐だから体積比が使えなくて困ってます Clear



1
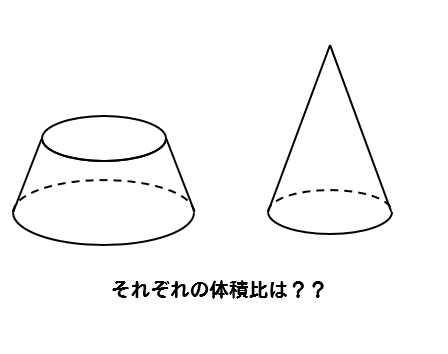



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



0 件のコメント:
コメントを投稿